The Doughnut Mode

Despite what you might think from its name, this is actually a real thing. It's something that you might see coming out of a laser. The doughnut mode is a stable laser beam that has a dark spot at its centre. End on, you would see a ring of light.

Side on, you can see that what you actually have is a tube of light with a dark core.

The beam in this image has been focussed by a lens--the doughnut mode can be focussed or manipulated in exactly the same way as a gaussian laser beam. The focussed doughnut mode is of greatest interest in atom optics.

If you look at what the wavefronts are doing in this beam, you can get some idea of why it has a dark centre. This is a picture of wavefronts in the doughnut mode.

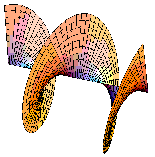
Along the central axis of the beam is a phase singularity. This is the sort of thing that we are interested in looking at close up.

How do we make them?

Although phase singularities like this occur naturally in laser beams, to study them, we really need to isolate them from all the other mess that the laser will output. A reliable way to create them is through the use of holography; we don't rely on natural generation in the laser. A hologram can be placed in front of a plane wave and one of the emergent beams will have a phase structure determined by the hologram.

All you have to do is calculate what the interference pattern between a doughnut mode and a plane electromagnetic wave. This is done fairly easily with a computer. The resulting pattern is then printed, and photographed onto normal slide film or holographic plates, and placed in the laser beam. For those with web browsers that support graphics, click on the picture for a full size version.

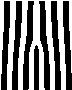Hologram to produce a doughnut mode with a charge one phase singularity. Note: Reference Heckenberg, et al.

How successful is this technique?

Press the button to see for yourself.

This is an image taken with a CCD camera of one of the first doughnuts that we made. The hologram was created by Shu-Yen Lee, who also took the picture.

Who's involved?

Faculty
- Dr. Robert Scholten scholten at optics.ph.unimelb.edu.au
- Dr. Ann Roberts
Students
- Julian Walford
- Shu-Yen Lee